摘要

本文论述了面广量大的光吸收类分析仪器研发、生产、使用中必须注重的几个关键理论，以及理论与实践结合的问题。讨论了透过率误差、吸光度误差和吸光度理论值或真值的关系、杂散光与吸光度相对误差A/A和吸光度真值A之间的关系、光度噪声N与吸光度相对误差ΔA／A和吸光度真值A的关系、光谱带宽（SBW）与分析检测误差的关系等等，同时提出了解决这些问题的方法和建议。

0、前言

由于分析仪器是“四两拨千斤”的产业，它在各国的国计民生中已经显示出五大作用：①科学研究的“先行官”；②工业生产的“倍增器”；③军事上的“战斗力”；④人类活动中的“物化法官”；⑤民生领域的“安全保证”等。所以可以说，分析仪器在“农、轻、重、海、陆、空、吃、穿、用”各行各业已经无所不在，无所不有。同时基于分析仪器在科技、经济、国防和社会发展中所处的重要战略地位等等，加速分析仪器产业的发展、生产已成为全世界各国关注的重点之一。

作者认为，全球分析仪器事业正处在日新月异、突飞猛进的变化时期。但是，全球的分析仪器行业还普遍存在一些理论问题，以及理论与实践相结合的问题。这些问题具体体现在没有解决好对仪器学理论的认识和理解、没有解决好在研发、制造、使用者中，真正重视仪器学理论和理论与实践相结合的问题上。本文为了保证研发者、生产者使用者能研发出优质分析仪器、使用者能真正用好分析仪器，作者将根据仪器学理论、分析化学理论和作者长期从事分析仪器研发、应用研究的实践经验、教训，从研发者、生产者和使用者的角度，从分析仪器的优质制造的更高要求的角度，以及分析仪器面临的紧迫使命等方面出发，寻找分析仪器行业优质制造中的问题，找差距、找瓶颈、找解决问题的办法，以保证我国分析仪器的优质制造，促使我国分析仪器更高速发展，尽快提高分析仪器的水平。

作者写本文目的是抛砖引玉，希望引起分析仪器领域研发仪器、制造仪器、使用仪器的广大科技工作者们的高度重视，并且积极参与讨论这些问题。希望大家共同为提高全球分析仪器，特别是提高我国分析仪器研发、制造、使用水平而努力奋斗。作者认为，分析仪器要振兴、要发展，就必须要注重并处理好本文提出的仪器学理论问题，必须处理好、解决好理论与实践结合的问题。本文可供分析仪器（特别是紫外吸收类分析仪器）的研发者、制造者、使用者和有关领导们参考。

1、透过率误差、吸光度误差和吸光度理论值或真值的关系^[1]-[15]

分析仪器的基础理论非常重要。分析仪器属于光、机、电、计算机和应用五为一体的、技术密集的高科技产品，涉及到的基础理论很多，如果不搞清楚其中的关键理论问题，大家闭着眼睛抓麻雀，或者是知其然不知其所以然，是不可能研发、生产出优质分析仪器的，使用者也不可能用好各类分析仪器、不可能得到准确可靠的分析检测数据。例如：紫外可见分光光度计（UVS）中的透过率误差△T与吸光度误差△A的关系，△T和△A与吸光度测量值Am、吸光度理论值A₀的关系[1]，杂散光（S.L.）与吸光度相对误差△A/A₀的关系[2]、[3]、[4]、[11]，光谱带宽（SBW）、噪声（N）与△A/A₀的关系^[3]等等。这些仪器学理论问题如果搞不清楚，既研发不出优质仪器，也用不好分析仪器。

目前，国际上许多UVS的研发者、生产者，在仪器的使用说明书中，一般都给出吸光度范围、吸光度误差和透过率范围、透过率误差等等，但是，都未搞清它们之间的关系，有些是随便写的。许多厂商，只要是自己认为是所谓高档UVS,就千篇一律的写为：透过率从0-100%T时（甚至更高），透过率误差（△T）都为0.3%T，这是不对的、绝对做不到的。而吸光度误差都写为： 0.002Abs（0-0.5Abs）和0.004Abs（0.5-1.0Abs）。这里的△T和△A₀是矛盾的，，绝大多数UVS生产厂商的产品都是如此，此现象很严普遍。对这个问题的研究工作，作者已经发表不少文章^{[1]、 [2]、[3]、 [4]、[15]}，请读者自己查阅。

透过率误差与吸光度误差和吸光度真值的关系，目前国际上很少有人系统的、认真的研究过。在这方面存在许多糊涂概念。作者对此作了深入研究，现在，我们来讨论透过率准确度、透过率误差与吸光度准确度和吸光度误差的关系，以及他们和吸光度真值A的关系。

作者从比耳定律的原始表达公式入手，认真研究了这些关系。比耳定律指出：

①A＝－logT，故T＝10^－A；

② C＝（－1/ab）logT, 故，T＝10^－abc；

①和②中：A为吸光度真值，T为透过率真值，a为摩尔吸光系数，b为光程，C为被测试样的浓度。

由此可见，A、T、C之间有着密切的关系。由于A或T的测量误差，可引起对被测试样浓度C的测量误差。若设T的误差为ΔT，则可求出不同ΔT的情况下，相对吸光度误差

ΔA/A (ΔA为吸光度真值A与测量值Am之差)与A的关系，或求出不同A下ΔA/A与ΔT的关系。

作者研究了ΔA/A与ΔT和A的关系，导出了ΔA/A与ΔT和A的关系之间的理论计算公式如下，它具有普遍的指导意义。

设：T－Tm＝ΔT          （1－1）

A－Am＝ΔA               （1－2）

（1－1）式、（1－2）中：Tm为透射比的测量值；Am为吸光度的测量值；由（1－1）式得：

Tm＝T－ΔT               （1－3）

根据比耳定律：A＝－logT，可得：

T＝10^－A                （1－4）

（1－4）式代入（1－3）式，得

Tm＝T－ΔT＝10－A－ΔT      （1－5）；

由（1－2）式得：

Am＝A－ΔA                （1－6）

根据比耳定律：Am＝－log Tm         （1－7）

（1－5）式代入（1－7）式，则：   

Am＝－log Tm＝－log（10－A－ΔT）     （1－8）

（1－8）式代入（1－6）式，则：

A－ΔA＝－log（10－A－ΔT）；所以，

ΔA＝log（10－A－ΔT）+ A              （1－9）

（1－9）式为吸光度误差ΔA与吸光度真值A和透射比绝对误差ΔT关系的理论计算公式。由此可见：

①ΔA与A和ΔT的数学关系式比较复杂；

②当ΔT一定时，ΔA可通过不同的A求得；。

③当A一定时，ΔA可通过不同的ΔT求得；

由（1－9）式可得到表1－1～7（因为篇幅冗长，此不赘述；请具体参阅：李昌厚著，《仪器学理论与实践》，北京：科学出版社，P176，2008），由表1－1～7可得下图、表。这些图、表是作者长期研究的经验总结，是一项从理论到实践的、非常重要的仪器学科研成果。在光学类分析仪器的设计、制造、使用和维修工作中很有参考价值，它可以适用于（或覆盖）全世界所有的紫外可见分光光度计。

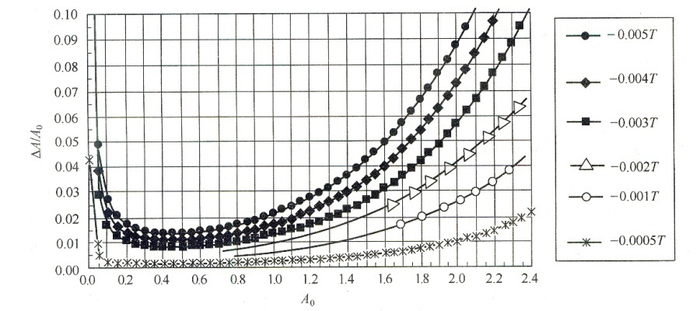
透过率误差ΔT与吸光度误差ΔA和吸光度真值A的关系

2、杂散光与吸光度相对误差A/A和吸光度真值A之间的关系^{[1]-[14]、[6]、[9]、[14] 、[15]}

作者对杂散光（S）进行了理论推导，得到了S与吸光度相对误差ΔA/A和吸光度真值A之间的关系为：ΔA＝log（Tm/T）＝log[（T+S）/T（1+S）]   

（令Tm＝（T+S）/（1+S）和S/T=10^A S

则ΔA＝log [（T+S） /T（1+S）]＝log [（1+10AS）/（1+S）]；

作者根据该计算公式，算出了14种常见的杂散光下，吸光度相对误差A/A和吸光度真值A之间的关系^[1]（如文献[1]中的表5－8所示；因为篇幅所限、表格太长，此处不能列出此表，请读者自己查阅）。作者根据表5-8，绘制了以下12条曲线。表5-8和这12条曲线非常重要、非常实用，是作者的一项重要科研成果。表5－8和曲线对紫外可见分光光度计的设计、制造、使用、维修者非常有用，它可以适用、覆盖全世界所有的紫外可见分光光度计。

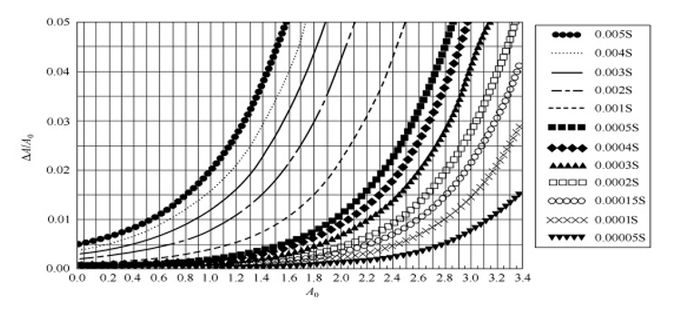
杂散光S与与吸光度相对误差A/A和吸光度真值A之间的关系

杂散光对紫外可见分光光度计分析测试误差的影响可分成两种形式，第一种形式是杂散光的波长与测试波长相同。它是由于测试波长因为某些原因而偏离正常光路，在不通过试样的情况下，直接照射到光电转换器上。引起这种杂散光的原因，大多数是由于光学元件、机械零件的反射和漫射所引起。这种杂散光可以通过一个对测试波长不透明的样品来检查。当发现放在比色皿中的不透明样品的透射比不为零时，说明仪器中有这种杂散光存在。但必须注意，当仪器存在零点误差时，有可能造成混淆。如果在不透明的样品上涂上白色，则可增加样品本身反射和散射的效果，可以提高测量灵敏度。

杂散光的第二种形式是指测试波长以外的、偏离正常光路而到达光电转换器的光线。它通常是由光学系统的某些缺陷所引起的，如光学元件的表面被擦伤、仪器的光学系统设计不好、机械零部件加工不良，使光路位置错移等等。

通常情况下，我们所讲的杂散光，是指包括上述两种杂散光在内的杂散光。假设Is为杂散光的总和，It为光电转换器检测到的总能量，它包括测试波长的能量I和杂散光的能量Is，即It＝I+Is。在实际分析测试工作中，我们需要知道的是杂散光能量Is相对于总能量It的比值。我们常称之为杂散光的量S＝Is/I_t。由于：

I » Is，因此，可以近似的认为It＝I，所以，可以认为S＝Is/I 。

S＝Is/I表示：当测试波长的能量降低时，杂散光比例就会相应增加。对紫外可见分光光度计的边缘波长来说，光源的强度、光电转换器的灵敏度和单色器的透过率都是比较低的，这时杂散光的影响就会更加明显。所以，在紫外可见分光光度计中，应该首先检查200～220nm处的杂散光。

我们知道，杂散光对参考光束和样品光束的影响是相同的。因此，根据比耳定律，可得到：A＝－log(It+Is)/(I+Is)；

因Is＝SI，

所以A＝－log（It+ SI）/（I+ SI）＝－log（It+ SI）/[I（1+ S）]

=－log[（It/I）+S] /(1+S)= －log(T+S) /(1+S)

=－log(T+S) + log(1+S)。

当T＝10％，S＝0％时，A＝－log0.1＝1

当T＝10％，S＝1％时，A＝－log（0.1+0.01）+ log1.01=0.9629

由此可见，当样品的透射比为10％时（即吸光度为1时），1％的杂散光，可使其吸光度从1.000降到0.9629。

同理：透射比为10%时，0.1％的杂散光，将使吸光度从1.000降到0.963。

一般使用者在紫外可见分光光度计的分析工作中，试样的吸光度都在1Abs以下，如果仪器的杂散光为0.05%时，对1Abs的试样测试时，测试误差仅为0.0019左右（见前述图、表）。因此，杂散光为0.05%时，就基本上能满足绝大部分分析工作的要求。如果紫外可见分光光度计的杂散光为0.01%时，杂散光对分析测试的结果就基本上没有影响了。

目前，国际上许多高档紫外可见分光光度计的杂散光都在0.01%以下。虽说杂散光0.01%时，杂散光对分析测试的结果就基本上没有影响了。但是，为了证明制造厂的加工水平，国外最高级的紫外可见分光光度计的杂散光达到8×10^－7（0.00008%），普析的国产最高级的紫外可见分光光度计的杂散光，达到了4×10^－7（0.00004%），处国际领先水平。杂散光对分析测试结果的误差影响是随着吸光度值增大而增大的。因此，吸光度值越大，对误差的影响也越大。如果吸光度A＝3（即T＝0.001），则杂散光为1%时，分析测试的结果将由A＝3变成A＝1.963（A＝－log（0.001+0.01）+ log1.01=1.9568+0.0043=1.963）。

由此可见，吸光度A＝3时，1％的杂散光可使分析测试的结果将由A＝3降到2以下。

作者的理论研究和长期使用紫外可见分光光度计的实践表明：当紫外可见分光光度计的杂散光为0.05%时，杂散光对分析测试误差的影响就很小了。这时，对吸光度为1.00A的试样进行分析测试，其结果为0.998A，相对误差为A /A＝0.002/1 ＝0.002（即0.2%）。所以，作者认为，从理论和实践结合的角度看，紫外可见分光光度计的杂散光为0.05%时，就基本能满足常规分析测试和质检工作的要求。

3、噪声N与吸光度相对误差ΔA／A和吸光度真值A的关系^{[1]、[4]、 [5]、[6]、[7]、[16]、[17]}

从理论与实践的结合上讲，光度噪声对分析测试误差的影响很大，必须重视之。在光度分析中，特别在紫外、可见光度分析中，可以说光度噪声是影响比耳定律偏离的最主要因素之一，它是紫外仪器最主要分析误差的来源。若已知光度噪声为N，则可根据A.J.Owen提出的计算公式：噪声误差（％）＝N100/A，计算出不同噪声N的情况下，吸光度的相对误差A/A（A为吸光度绝对误差，A为吸光度真值）与A的关系，或求出不同A的情况下，A/A与N的关系。

例如：若紫外可见分光光度计的噪声N＝±0.002A，吸光度真值为0.5A，则：根据A.J.Owen提出的计算公式，噪声误差（％）（即由噪声引起的相对误差AN/A）＝0.002×100/0.5=0.2/0.5=0.4(%)。，即由噪声引起的相对误差AN/A为0.4%。

目前国内外的紫外可见分光光度计制造者和使用者们，很多都不注重仪器的光度噪声。他们并不了解光度噪声对使用者的分析测试结果有多大的影响。、，很少有人从理论上或从理论与实践结合的角度，对此进行认真的研究。有的厂商甚至在样本上不给出光度噪声这个重要指标，有些厂商（技术人员）在测试光度噪声时只测3分钟或15分钟，最多的只测30分钟。这些都是不对的，都是很值得注意的重要问题。

作者认真研究了光度噪声N与吸光度的相对误差A/A和吸光度真值A的理论关系，从理论上计算了N与A/A和A的关系。作者研究的结果如文献[1]的表5－10～15所示，因为篇幅所限、表格太长，此处不能列出此表，请读者自己查阅。作者还根据文献[1]的表5－10～表5－15，绘制了12条误差曲线，如下图所示。这是作者多年研究的科研成果，它可以覆盖目前世界上任何不同类型的紫外可见分光光度计，该成果对设计、制造、使用和维修者具有重要的实用参考价值。

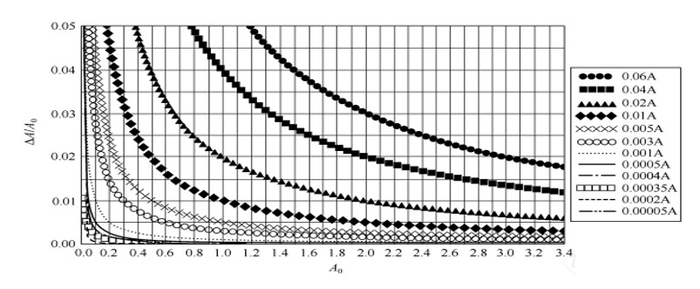
噪声 N与吸光度相对误差ΔA／A和吸光度真值A的理论关系

4、光谱带宽（SBW）与吸光度误差（分析检测误差）的关系

1）SBW的定义：光谱仪器的单色器出射狭缝谱面上的光谱数，就叫SBW。

若以谱线轮毂法（一种测试方法）表示，则51%峰高处的谱线宽度，就是SBW。具体描述，可见下图所示。

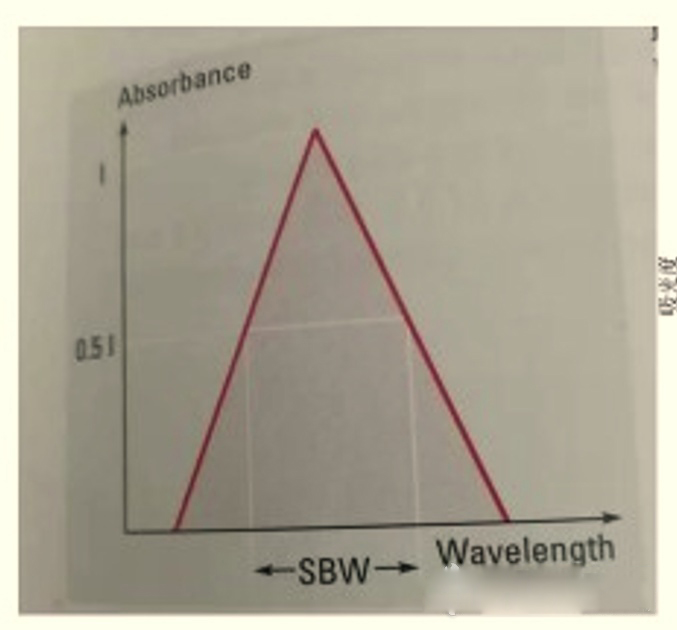
光谱带宽(SBW)是非常重要的技术指标，它直接影响分析测试数据的准确度。作者^[1]和Owen ^[5]对SBW做了比较深入的研究，因篇幅所限，请读者自己查阅，此不赘述。

2）光谱带宽对吸收光谱测量误差关系的理论推导：

光学类的分析仪器中，光谱带宽非常重要。不同的样品要求用不同的光谱带宽测试，对同一样品，不同的光谱带宽有不同的分析误差。每一个样品，都有自己的最佳光谱带宽，只有在最最佳光谱带宽下才能得到最佳的分析数据。

从理论上讲，比耳定律只适用于单色光，但在实际的吸收光谱仪器中，绝对不可能从光谱仪器的单色器上得到真正的单色光，只能得到波长范围很窄的光谱带。因此，进入被测样品的光束仍然是在一定波段范围内的复合光。由于物质对不同波长的光具有不同的吸光度，因此，在实际工作中即使用很高级的吸收光谱分光光度计、采用很小的光谱带宽，仍然会产生比耳定律的偏离（即产生吸光度测量误差）。

作者根据仪器学理论，对光谱仪器的SBW从理论上作了详细研究^[1]。作者研究表明：假设SBW为Δλ，它所对应的波长范围为λ1∽λ2 。对λ1而言，设其入射光强度为I01 ，透射光强度为I1 ，摩尔吸光系数为ε1 ，吸光度为A1，则：

A1＝lg I₀₁/I₁=ε₁bc；I1＝I₀₁×10^－ε1bc

对λ2而言，设其入射光强度为I₀₂ ，透射光强度为I₂ ，摩尔吸光系数为ε₂，吸光度为A₂，则：A₂＝lg I₀₂/I₂=ε₂^bc， I2＝I02×10^－ε2bc

因在实际测量时，对应的入射光强度为I₀₁+ I₀₂ ，透射光强度为I₁+I₂ 。 因此，吸光度值为：

A= lg （I₀₁+ I₀₂）/（I₁+I₂）

＝lg （I₀₁+ I₀₂）/(I₀₁×10^－ε1bc+ I₀₂×10^－ε2bc )        (4-1)

若ε₁＝ε₂＝ε， 则 (4-1) 式可写成：

A= lg 【（I₀₁+ I₀₂）/（I₀₁+I₀₂）×10^－ε1bc 】＝lg （1/10^－ε1bc）

＝lg10^εbc＝εbc。

此时，A与C成线性关系。

但实际上，摩尔吸光系数ε是有色物质的与波长有关的特征常数，对同一有色物质而言，不同波长有不同的ε值。在实际测量中，常取某一光谱带宽，它对应的波长范围为λ1∽λ2   ，λ1和λ2各对应ε1和ε2 ，但ε1和ε2 不可能完全相等。所以，在吸收光谱仪器中，对某一光谱带宽的入射光，A与c不可能真正成线性关系。由于光谱带宽的影响，产生了比耳定律偏离，或产生了分析测量误差。

3）光谱带宽对吸收光谱分析测量误差的影响：

设ε1〉ε2 ，并且，对选定的仪器而言，常规分析时，光程b是常数，被分析样品的浓度是变数；若将 (4-1)式相对bc微分，则：

dA/d(bc)=ε1－[(I₀₂ /I₀₁) ×(ε₁－ε₂) ×10^{（ε1－ε2）bc]}/[1 +

（I₀₂ /I₀₁）×10（^{ε1－ε2）bc}]         (4-2)

当试样的吸光度非常小时（bc→0），则：

dA/d(bc)= [ε1+（ I₀₂ /I₀₁）×ε₂]/[1+( I₀₂ /I₀₁)]   (4-3)

当试样的吸光度很大时（bc→∞），

(4-2)式中的10ε1bc   » 10ε2bc ，则：

dA/d(bc) =ε2                 (4-4)

因为光谱带宽一般都很小，所以，Δλ对应的λ1∽λ2 的光强度一般也相差甚微。或者说几乎相等。则：（I₀₂ /I₀₁）=1；则： (4-2)式可写成：

dA/d(bc) =（ε₁+ε₂）/2           (4-5)

从 (4-4)、 (4-5)两式，可以清楚看出：在低吸收时，仪器测得的A－C曲线的极限斜率是ε1和ε2的均值；而在高吸收时，极限斜率是ε₂ 。显然，ε₂<[（ε1+ε₂）/2] <ε₁ 。 因此，在低吸收时，测量误差较小，在高吸收时，测量误差较大。这是光谱带宽影响的结果，广大分析工作者应特别引起注意。

光谱带宽对吸收光谱测量误差的影响可以根据下式计算：

A obs =log∫IλSλdλ/ IλSλ10－^Adλ                ( 4-6)

(4-6))式中： A obs为实测吸光度值，Iλ为入射光强度，Sλ为光接收器的光谱灵敏度，A为吸光度理论值（真值）。

式（4-6）说明了实测吸光度值不但与吸收曲线（A－C曲线）的形状有关，而且与光源的波长分布、光接收器的光谱响应特性有关。在实际测量工作中，对已选定的仪器来说，在同一光谱带宽内，入射光强度和光接收器的光谱灵敏度是一个常数。

实际分析检测工作中，光谱带宽对分析检测结果影响很大，直接影响分析检测数据的可靠性。例如下图示，两个很好的峰，由于选择的光谱带宽不同，分析检测的结果相差很大，最坏的情况是两个检测峰变成了一个峰。如下图所示，当用1nm光谱带宽测试时，可得出一个很漂亮的光谱图；还是这台仪器、还是这个样品、还是这个分析工作者，当他分别改用5nm、10nm、20nm、50nm光谱带宽测试时，得到的谱图，明显比用1nm光谱带宽测试的峰高低很多。在20nm光谱带宽测试时，两个很漂亮的峰就变成了一个马鞍形的峰。特别在50nm光谱带宽测试时，1nm光谱带宽测试时的两个峰就变成一个馒头峰。由此可见，光谱带宽对分析测试误差有多大的影响。但是，目前国内外广大分析工作者还远远没有认识到光谱带宽是紫外可见分光光度计分析误差的主要来源这个非常重要的问题。

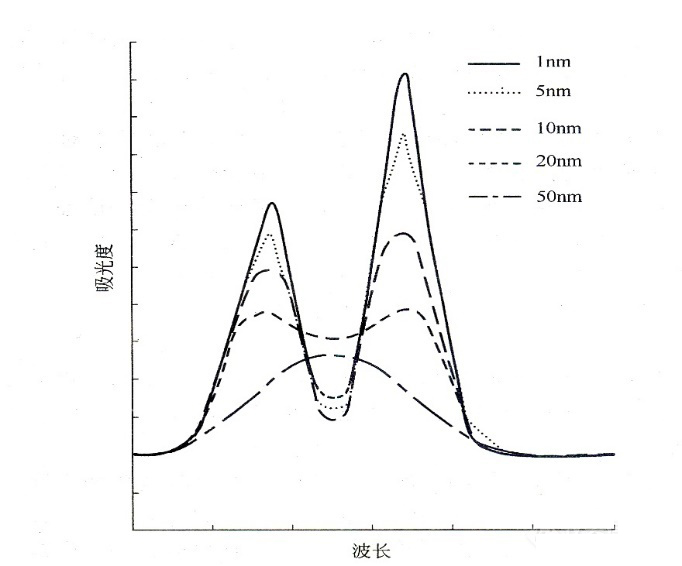
作者从理论上证明了光谱带宽会引起吸收光谱仪器的分析测试误差，并给出了计算公式。目的是想以此引起广大分析工作者重视对光谱带宽问题的重视，以便提高分析测试结果的可靠性、提高分析测试技术水平。

5、分辨率的物理概念及其重要性

分辨率定义：

如下图所示，两条等高的峰，能够分到80%高度时，就被认为分开了，这就是著名的瑞利准则。但是两条完全相等的谱线是没有的。同时为了便于测试，若从光谱带宽的角度考虑，从谱线轮毂法（下图右）表示，人们定义了最小光谱带宽就是分辨率。如果光谱带宽固定，则该光谱带宽就是分辨率。

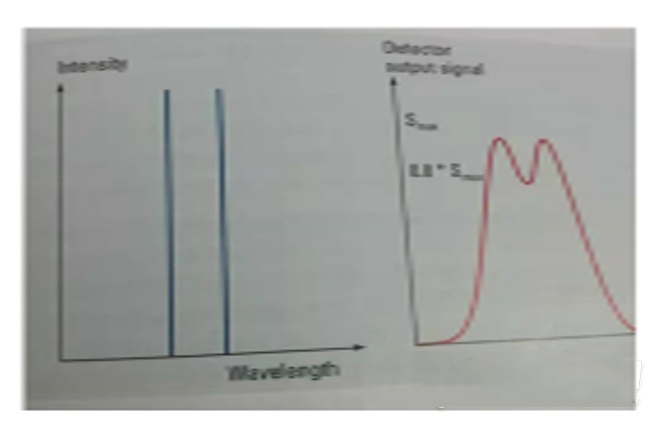
分辨率决定了光谱仪器能够分开两条谱线的能力，特别是在较复杂的样品分析检测时，仪器的分辨率显得非常重要。所有从事分析检测工作的科技工作者都应该对此引起重视。

6、结束语

长期以来，我国的仪器制造厂商和国外有关的仪器厂商一样，大家生产的很多光吸收类的分析仪器，给出的△T都是错误的、△T和△A都是自相矛盾的。有的厂商不给N、不注重对SBW的研究等，就是不注重对分析仪器的基础理论研究的结果。因此，作者认为，我们国家有关部门和工厂企业、研究者、制造者和使用者们，都应高度重视分析仪器的理论问题，并且用以指导实践。大家千万不要满足低水平的重复，不能闭着眼睛捉麻雀。只有在实践中重视分析仪器的理论问题，并在实践中注重理论和实践的结合，知其然知其所以然，才有可能制造出高质量的分析仪器。只有这样，才能进一步提高分析仪器的水平。因此，作者认为：在仪器学领域、在理论和实践的关系上，首先要重视仪器学理论和分析化学理论，同时重视理论和实践的结合，这才是提高分析仪器水平的重要基础和途经，才有可能尽快赶超国际分析仪器的先进水平。

7、主要参考文献

[1]李昌厚著，仪器学理论与实践，北京：科学出版社，2008。

[2]M.R.Shape,Stray Light of UV/VISS, Analytical Chemistry, Vol.56, No.2,p339A,1984

[3]李昌厚，杂散光与吸光度相对误差关系的研究，中国仪器仪表学报，53，1，2001.

[4]李昌厚，略论比耳定律及其有关问题，光学仪器，4，20，1984。

[5] A. Owen ,The diode-array advantage in UV/VISS,Hewllet Packrd,PrinnTED in Germany,03/88,p15.

[6]Wensted，lnstrument Check Systems,Published in Great Britain by Hencry Kimpton Publishers London,1971.

[7]Li chang hou,’99 Industrial instrumentation and automation conference,Internationalinstrumentation and automation(specialsupplement) ,p257,1999.

[8]李昌厚，论中国分析仪器的十大关系，科学时报（科学装备B1版），2001年5月.

[9]瓦里安, CAry 6000i UV/VIS/NIRSpectrophotometer,说明书

[10] Shimadzu,2401PC/2501PC 紫外可见分光光度计（样本）

[11]李昌厚，透光度误差与吸光度误差关系的研究，现代科学仪器，25，1，2000

[12]李昌厚，提高可靠性，迈上新台阶，科学时报（科学装备B1版2000年11

[13]Tony Owen, Fundamentals of UV-Visible Spectroscopy, Printed in Germany 09/96,(HP puplication number 12-5965-5123E), P106, 1996

[14]李昌厚著，紫外可见分光光度计，北京：化学工业出版社，2005

[15]李昌厚著，紫外可见分光光度计及其应用，北京：化学工业出版社，2010

[16]李昌厚著，原子吸收分光光度计，北京：科学出版社，2006

[17]李昌厚著，高效液相色谱仪器及其应用，北京：科学出版社，2014

本文转载自网络,如有侵权,请留言联系我进行删除,谢谢!